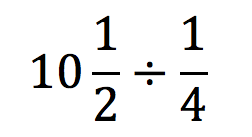How Do You Assess Number Sense?

My instinct is, “I know it when I see it”.

I want to move beyond that. My school loves to talk about “basic skills”. Basic skills are usually interpreted as rational number operations — decimals, fractions, positives and negatives. Then these are tested using numbers requiring several steps of calculation. But, in Algebra, lots of those basic skills become less important. Students aren’t often operating with decimals and fractions, and doing multi-digit whole number operations. When they are, they often have a calculator — as they should, to minimize the working memory load as they struggle with abstract concepts.

So I’m skeptical about the value of reteaching basic skills. I have students who struggle with simple fraction operations. But they’ve learned fraction addition several times before my class. What do I know that will allow me to teach them better, so they suddenly learn it and remember it — despite the fact that I don’t have as much time, they won’t get as much practice, and won’t see it on a regular basis as they did the first few times around?

So this is an attempt to create something better. I’m not sure I have a great definition for number sense, but one big part of it is a variety of strategies to solve simple problems based on number relationships. These relationships are the building blocks of Algebra — students don’t need to add mixed numbers with unlike denominators, they need to understand the relationship between multiplication, division, and the fraction bar. Students don’t need to divide 1963 by 21, they need to see the power of the commutative property of addition. These are half-formed ideas, but they start to get deeper than “I know it when I see it”.

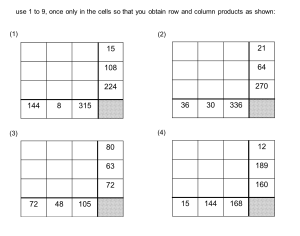
So here’s a crazy idea. I broke number sense down into three categories — whole numbers, rational numbers, and ratios & proportions. Then I built an assessment. Each item was a simple calculation, comparison, or estimation. Each could easily be solved using familiar algorithms. But, each could also be solved, in some cases much more easily, without an algorithm. I’m curious: first, how many questions students will get right (I teach 8th grade, and everything here falls in 6th grade or earlier, I believe). Second, how many questions students will solve using strategies that show an understanding of number relationships, not just algorithms. This is imperfect (for instance, I realized the last question is vague). But I gave it to two of my best students today, and I was fascinated by some of their work. Here are two students’ answers.

Student 1:
   

Student 2:

What does this work show about these students’ number sense? How can it be useful? I’m not sure. I love looking at this stuff, but these two students both got everything or almost everything right. I’m not sure this is so different from the basic skills I want to push away from — but it worries me a bit that these students regrouped to subtract 1001 – 993. I was worried that one used long division to find a decimal approximation for 3/7 to confirm that it is smaller than 1/2. Should I be concerned? Is it possible those are “false negatives” — is the first student showing work because she thinks she should, or because she needs to?

So many questions. I’m going to give this to a few more students and adults over the next few days, and see what I can learn.

[If you’re interested in a soft copy of the current version of the assessment, it’s here]

Number Talks and Factoring

One of the skills that’s key to number sense, and is even more evident in many number talks, is flexibly breaking numbers apart and putting them back together. For instance, when asked to multiply 21 by 15 mentally, students who are most successful think about it as 21×10 + 21×5,  or 15x7x3, or 21x5x3, or 15x10x2 + 15.

These skills — formally, factoring numbers and using the commutative, associative, and distributive properties — are often glossed over in impenetrable language, or memorized for a test as 7×5 = 5×7, and then forgotten. And the skills are subtle ones that are hard to teach in a single lesson — they are skills that make math easier, but are rarely absolutely necessary to solve a problem — only to solve it well, or solve it in a new way.

I recently came across two resources that I really like to address these skills. From Don Steward, these puzzles:

and from Visualizing Math (although this was all over the internet when I searched for it, I just saw it first there), the chicken nugget problem:

These both struck me as questions that a) don’t fit neatly into any middle school math objective, b) have embedded in them incredibly rich practice breaking numbers apart and putting them together, and c) are puzzling.

This math gets at the hazy, nebulous idea of concept development that is so hard to facilitate and plan for. In particular, finding a place for these problems so that students can access them, but still find that sweet spot to develop the concepts that students need to be thinking about as they dive deeper into mathematics.

Number Sense – Long Distance Hiking

Did a mini 3-act task today. Showed my students a bunch of pictures of the High Sierra where I’ll be hiking on the John Muir Trail this summer, for instance:

(I’m really really excited about this trip)

Anyway, then I took a few questions, and we looked at some maps. I told them I plan on hiking close to 300 miles, and asked how long they thought it would take.

Answers ranged from 2 days to 3 months, which I was pretty fascinated by. Most students were in the 1-2 week range — way faster than I’ll be hiking, but within the scope of reason — in particular for kids who usually move around the world much faster than that.

Then students had to name the information they needed to solve. They all knew they needed speed, but there was some interesting discussion about the remaining variable. Once we nailed down that I would only hike for some of the day, I told them I expected to hike about 2 miles per hour, and that I would hike from 7:00 am to 6:00pm with 3 hours of breaks in between.

Here, students struggled mostly to keep their work organized. They work well with distance, speed and time — they have several methods to work with, in particular proportions or d = rt — and had all the pieces. Got some really interesting answers. I really liked one girl who got 18.75 days, then told me that it would take 18 days and 18 hours. We then had a fun conversation about what that meant about the time I would finish.

We did several more similar examples as a class, then more practice on their own, variants of the above talking about road trips or bike tours. I really emphasized organization of work, and pushed something I haven’t before — drawing a vertical line to divide the workspace when solving a multi-step problem. One of our 7th grade teachers has done an incredible job with this, and I’m excited to teach her students next year with that in the toolbag. I don’t love telling them exactly how to solve a problem like this one, but organized and well-labeled work will be an asset to them in a huge range of academics, and I’ll be excited if I see students continuing that organization.

Also, great moment during student practice — a student solved a problem about a cross-country road trip. They were driving slowly — 5 hours per day to see the sights — and took 11 days to cross the country. She was really concerned that it took so long to get from the east coast to the west coast! Loved that she was able to be metacognitive about the problem.

All in all a fun lesson. Next time I need to connect their curiosity about my trip more concretely to the mathematical questions at hand, and try to find some more graphics and representations to give kids a foothold in what’s actually happening.

Number Sense – How Many Graduates?

My little sister graduated from Boston College yesterday, and the whole family was in town to celebrate. Of course, I couldn’t resist taking a moment to snap a few shots for an estimation task:

How many students graduated from BC?

(I don’t know the answer; none of the speakers mentioned it)

But check out the full graduating class:

And the crowd:

 

Estimate away!

 

 

Number Sense – Factoring

Loved this post from Don Steward, offering these number puzzles:

Really enjoyed playing with these– they have some fascinating properties and can be solved efficiently only through a pretty deep understanding of prime factorizations. It’s one of those topics that students tend to either “get” early on, or they memorize it and forget it in 6th grade. I’m curious what other parts of math this type of thinking supports.

Number Sense – Number Talks 5/16

Number talk today:

Many kids found the precise answer within a minute, and there weren’t major misconceptions from the students who shared. That said, the big idea I’m looking for in most multiplication number talks — effective use of the distributive property — didn’t come from as many kids as I would’ve hoped. There were basically three camps:

1. Students who found creative ways to multiply — for instance 51 x 9, then double the answer, or rounding 18 or 51, or 51 x 6, then triple the answer. All great strategies, but not quite what I was hoping would come out.
2. Students who made use of the distributive property (usually by finding some way to calculate 18 x 50, then adding one more 18), but didn’t make that clear from their explanation.
3. Students who used the distributive property, but were clear about breaking apart (for instance) the 51 into 50 and 1, and multiplying the two parts separately.

I would estimate students were about 30% using #1, 60% using  #2, and 10% using #3.

This isn’t a big misconception, but students will be more powerful mathematicians if they can name and work flexibly with the distributive property.

Today made me think more about the way I scribe answers. Starting in my second class, I made a significant effort to probe students to be more explicit about their use of distribution, and to scribe it in a way to help other students make sense of it. I’ve had a desire to give more student ownership to number talks — for instance student scribes, or more partner-based interactions. But today reminded me of the value I have as the teacher — of taking a mathematical concept that one student is using effectively, and making it clear and accessible to the rest of the class. That’s not the student’s job; it’s mine. The best way to make that happen, however, is something I’m still working on.

Number Sense – Dots and Powers of Ten

Number Talk Today: How many dots in this image?

 

Huge variety of answers. Three observations:

• No student (or at least no student who wanted to share) saw it as a 10×10 box with 4×3 and 5×4 pieces cut out. Not a big deal, but I thought that was interesting.
• Many students saw it a a series of rows or columns, rather than overlapping/adjacent rectangles. I think this speaks to the lack of number sense I see — they don’t have fluency with rectangular representations of multiplication. Still plenty of students who did, but there was a pretty sharp divide between the two groups in all of my classes.
• My students love dot patterns. It’s awesome to see them all counting the heights of the rows and columns, and in some cases leaning up out of their chairs to make sure they count right. I would say classes averaged about 2/3 of students who wanted to share their approach. Also, classes ranged from 4 – 8 different answers at the start (I’ve been starting by taking every answer anyone has, with no judgment given on the quality of these answers). Again, speaks to their lack of fluency with rectangular representations of multiplication, and in 8th grade!

I’ve thought more about the idea of longitudinal structure to number talks. I’ve only been doing them for a few weeks, but they’re my favorite part of class. My students in general don’t love doing what I ask them to do, but engagement is high during number talks and almost everyone has volunteered to speak at one point or another, including the vast majority of my lowest-skilled students.

Anyway, I’ve been thinking a lot about next year. Between losing a few classes as students take finals and a 4-day trip to Washington D.C. I don’t have much time left with my current crew, but I’m excited to figure out how to make number talks even more awesome for next year.

Here’s my idea of the day, which I’m sure will change radically by the time I implement it.

1. Students will have a weekly sheet that they keep with them to track number talks.
2. Each week there will be a theme to number talks — multiplication, division, dot patterns, spatial sense, “does this answer make sense”, estimation, and more.
3. Students will still do the math mentally, share all answers, then share strategies, but while sharing strategies, students will have the chance to scribe strategies they like.
4. At the end of each number talk, students will write the strategy they liked best, or, if they liked their own best, why they preferred it to others.
5. At the end of the week, students will have an additional few minutes to write what they learned from the number talks that week, and note any strategies that were new to them that they will use in the future.

Finally, we we’ll be talking about exponents and scientific notation today. I opened with this oldie but goodie from 1977 on the powers of ten and the universe. I stopped it after it reach it’s outer limit, and tomorrow we will watch it zoom all the way into a proton. The questions I got were interesting — mostly around the speed of light and being awestruck at the size of the universe.

 

 

Number Sense – Exponents Number Talk 5/14

This number talk today, inspired by Michael Pershan’s posts on exponents:

• A student in every class shared the perspective that it was 5 cubed.
• Most students multiplied 5s, but did not talk about exponentiation — instead it was 25 groups of 5, or 5 groups of 25, or other patterns
• A few students had some really creative ways of breaking down the pattern into 5s –try and figure out

8 + 9 + 2*4
4*4 + 1 * 4 + 4
4*4 + 2*2 + 5

• I was really impressed with several students who shared strategies that were a bit slower, for instance counting every group of 5, without shame. I hope I can keep that culture going.

My students have already seen exponents for a few years (I teach 8th grade), and I’m curious how this would develop thinking differently for students who haven’t articulated the idea of an exponent. There’s definitely some element of intellectual need for it, but at the same time it doesn’t scream “this will make your life easier in the future”, which is something I want students to see when exploring a new concept.

Either way, kids really liked this, and there aren’t enough great visualizations of exponents out there. I’m excited to show them this one:

Number Sense – Number Talks 5/13

Number talk today:

Got a lot of great ideas. A few that struck either me or my students:

• Several students doubled, and then doubled again to make multiplying by 4 easier
• Using the distributive property to break apart 10 and the half seems like common sense, but it was a big hit in two classes. I’m beginning to think that a flexible understanding of the distributive property is a huge part of number sense
• Among students who prefer to operate with improper fractions, there is a divide between students who see the opportunity to simplify the fraction first (21/2 * 4/1 = 21/1 * 2/1)  rather than multiplying (one student converted to a common denominator of 4, for 84/4, then multiplied 84 * 4 and divided by 4*1). These are the valuable shortcuts that a) make calculation easier, but b), and more importantly, show an understanding of algebraic structure, in particular the critical importance of the commutative and associative properties when working with fractions.

On this note, I’ve been thinking more about the longitudinal structure of number talks. I’m structuring them day by day pretty randomly — whatever I think will be meaningful is what we think about. I’m curious if grouping them by structures I want students to see would be valuable. On the one hand, sustained practice with a mathematical idea could help solidify that idea, especially in lower-skilled students. On the flip side, math is math, and number talks as mixed practice have a lot of value in messaging math for math’s sake. On top of that, I’m not sure students could keep track of a weekly theme for number talks, the unit we’re in for the rest of class, and then a range of topics for warm-ups and the rest of their classes in a meaningful way. But maybe it’s something to think about.

Number Sense – Who Has It?

A few tangents tonight. This great post from Number Loving Beagle got me thinking, in particular this piece:

I hear occasionally from teachers that we need to teach kids “responsibility” and we can’t force them to learn if they don’t want to.  This line of thinking bothers me a great deal as places the burden of being eager to learn on the student.  Some kids place “learning at school” very low on their priority list.  We must acknowledge that rather than disregard it with “he/she never came and asked a question.”  If we are being honest with ourselves, we know exactly which kids need the help but won’t outwardly seek it.  We know which kids won’t ask questions when they have them, and which ones won’t make an effort to turn in assignments that they’ve missed.   It’s not that they are incapable of seeking help, asking questions, and turning in assignments.  But by stating that “help was offered but not taken” we do not absolve ourselves from the responsibility to reach these students.

I’ve been guilty of this. It perpetuates the haves/have nots divide in students — those who are invested in school, see the positive effects of their hard work, and continue to work hard for their education; and those who struggle to get invested and are continually discouraged by negative feedback and internalize that they are out of control of their learning. That’s one big issue, and one I care a lot about, as I think my biggest failures this year have been in a few students I’ve struggled to give reasons to engage in my class.

This got me thinking about number sense as well. We talk about number sense in these same terms — either students have it or they don’t, and especially in upper middle school we give little thought to teaching number sense. When we do “teach” number sense, it’s often asking students if their answer makes sense, or showing students a  shortcut, or giving students worksheets of “basic skills” (decimal and fraction operations).

But students who have number sense gained it by making sense of math problems — by constantly checking their thought process and their answers against a mental image of the problem and solution space, by using multiple representations to understand a concept, by estimating quickly and strategically. Asking students who struggle with these skills to do them without support is asking them to fail and revert to their answer-getting ways that have got them this far.

So what does a lesson look like that supports all students, no matter where their number sense is? I have no idea. Number talks are all I have right now, but I’m looking.