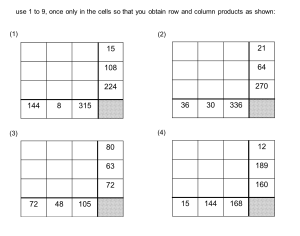
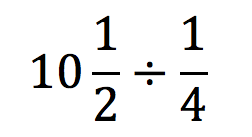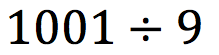Number Talk: Tax

Number talk today:

A pair of jeans is priced at $60, and is taxed at a rate of 8.5%. How much will the jeans cost, with tax?

New best practice: Ask for estimates first. I usually take every answer to start a number talk, but this can result in estimates becoming less valid, because students can tell both from which students share and the collective response of the room which answer is right. While I try to emphasize that estimates are often just as good as exact answers, I don’t think the kids buy it yet. Today, I asked for estimation strategies first, before allowing any students who thought they found an exact answer.

Thing I learned: Kids will do some weird stuff with numbers, and I don’t always know how to respond to it. One kid multiplied 6×8, then 6×5, then added and told me the answer was $78 (at least it was more than $60!). Another tried to multiply by 1.85, which had the spirit of a right answer, but showed a lack of sense for how big the answer should be. How do you facilitate that conversation? Have other students steer them back? Linger on the misconception, or try to move on quickly?

Thing not many students did: I mean, plenty did it, but I was hoping to see more say $66. Between errors and students who tried to get more precise, I didn’t get many kids with $66.

My favorite strategy: 10% = 6. 2% = 1.20. .5% = .30. 10 – 2 + .5 = 8.5. 6 – 1.2 + .3 = 5.10. Answer is $65.10.

This was a fun one, but I need to work on making estimation, and estimating with friendly numbers, a go-to strategy for my students.

Number Talk – Phone Battery

Had a fascinating experience with a number talk last week. Question was:

After 3 hours, your phone battery is at 93%. How long do you expect it will last before it dies?

I was fascinated and concerned by the students answers:

A small but significant number of students used estimation or proportional reasoning strategies to arrive at an answer.

A large number of students didn’t calculate — they said that the initial situation was unreasonable, and the battery would be much lower. They all made estimates based on their own experiences, separate from the question asked.

The final group, which was the largest, told me — with complete confidence — it will last 31 hours, because 93 / 3 = 31.

I shouldn’t have been surprised, but I was — in particular by their confidence. It’s a huge problem in number sense — the belief that every question with two numbers is either addition, subtraction, multiplication or division. And given that belief, what they did makes sense — the other three operations clearly give answers that are unreasonable, and 31 hours isn’t too far off.

Still, I’m adding it to my list of things I want to fix through number talks and number sense activities this year.

Number Talks and Factoring

One of the skills that’s key to number sense, and is even more evident in many number talks, is flexibly breaking numbers apart and putting them back together. For instance, when asked to multiply 21 by 15 mentally, students who are most successful think about it as 21×10 + 21×5,  or 15x7x3, or 21x5x3, or 15x10x2 + 15.

These skills — formally, factoring numbers and using the commutative, associative, and distributive properties — are often glossed over in impenetrable language, or memorized for a test as 7×5 = 5×7, and then forgotten. And the skills are subtle ones that are hard to teach in a single lesson — they are skills that make math easier, but are rarely absolutely necessary to solve a problem — only to solve it well, or solve it in a new way.

I recently came across two resources that I really like to address these skills. From Don Steward, these puzzles:

and from Visualizing Math (although this was all over the internet when I searched for it, I just saw it first there), the chicken nugget problem:

These both struck me as questions that a) don’t fit neatly into any middle school math objective, b) have embedded in them incredibly rich practice breaking numbers apart and putting them together, and c) are puzzling.

This math gets at the hazy, nebulous idea of concept development that is so hard to facilitate and plan for. In particular, finding a place for these problems so that students can access them, but still find that sweet spot to develop the concepts that students need to be thinking about as they dive deeper into mathematics.

Number Sense – Number Talks 5/16

Number talk today:

Many kids found the precise answer within a minute, and there weren’t major misconceptions from the students who shared. That said, the big idea I’m looking for in most multiplication number talks — effective use of the distributive property — didn’t come from as many kids as I would’ve hoped. There were basically three camps:

1. Students who found creative ways to multiply — for instance 51 x 9, then double the answer, or rounding 18 or 51, or 51 x 6, then triple the answer. All great strategies, but not quite what I was hoping would come out.
2. Students who made use of the distributive property (usually by finding some way to calculate 18 x 50, then adding one more 18), but didn’t make that clear from their explanation.
3. Students who used the distributive property, but were clear about breaking apart (for instance) the 51 into 50 and 1, and multiplying the two parts separately.

I would estimate students were about 30% using #1, 60% using  #2, and 10% using #3.

This isn’t a big misconception, but students will be more powerful mathematicians if they can name and work flexibly with the distributive property.

Today made me think more about the way I scribe answers. Starting in my second class, I made a significant effort to probe students to be more explicit about their use of distribution, and to scribe it in a way to help other students make sense of it. I’ve had a desire to give more student ownership to number talks — for instance student scribes, or more partner-based interactions. But today reminded me of the value I have as the teacher — of taking a mathematical concept that one student is using effectively, and making it clear and accessible to the rest of the class. That’s not the student’s job; it’s mine. The best way to make that happen, however, is something I’m still working on.

Number Sense – Dots and Powers of Ten

Number Talk Today: How many dots in this image?

 

Huge variety of answers. Three observations:

• No student (or at least no student who wanted to share) saw it as a 10×10 box with 4×3 and 5×4 pieces cut out. Not a big deal, but I thought that was interesting.
• Many students saw it a a series of rows or columns, rather than overlapping/adjacent rectangles. I think this speaks to the lack of number sense I see — they don’t have fluency with rectangular representations of multiplication. Still plenty of students who did, but there was a pretty sharp divide between the two groups in all of my classes.
• My students love dot patterns. It’s awesome to see them all counting the heights of the rows and columns, and in some cases leaning up out of their chairs to make sure they count right. I would say classes averaged about 2/3 of students who wanted to share their approach. Also, classes ranged from 4 – 8 different answers at the start (I’ve been starting by taking every answer anyone has, with no judgment given on the quality of these answers). Again, speaks to their lack of fluency with rectangular representations of multiplication, and in 8th grade!

I’ve thought more about the idea of longitudinal structure to number talks. I’ve only been doing them for a few weeks, but they’re my favorite part of class. My students in general don’t love doing what I ask them to do, but engagement is high during number talks and almost everyone has volunteered to speak at one point or another, including the vast majority of my lowest-skilled students.

Anyway, I’ve been thinking a lot about next year. Between losing a few classes as students take finals and a 4-day trip to Washington D.C. I don’t have much time left with my current crew, but I’m excited to figure out how to make number talks even more awesome for next year.

Here’s my idea of the day, which I’m sure will change radically by the time I implement it.

1. Students will have a weekly sheet that they keep with them to track number talks.
2. Each week there will be a theme to number talks — multiplication, division, dot patterns, spatial sense, “does this answer make sense”, estimation, and more.
3. Students will still do the math mentally, share all answers, then share strategies, but while sharing strategies, students will have the chance to scribe strategies they like.
4. At the end of each number talk, students will write the strategy they liked best, or, if they liked their own best, why they preferred it to others.
5. At the end of the week, students will have an additional few minutes to write what they learned from the number talks that week, and note any strategies that were new to them that they will use in the future.

Finally, we we’ll be talking about exponents and scientific notation today. I opened with this oldie but goodie from 1977 on the powers of ten and the universe. I stopped it after it reach it’s outer limit, and tomorrow we will watch it zoom all the way into a proton. The questions I got were interesting — mostly around the speed of light and being awestruck at the size of the universe.

 

 

Number Sense – Exponents Number Talk 5/14

This number talk today, inspired by Michael Pershan’s posts on exponents:

• A student in every class shared the perspective that it was 5 cubed.
• Most students multiplied 5s, but did not talk about exponentiation — instead it was 25 groups of 5, or 5 groups of 25, or other patterns
• A few students had some really creative ways of breaking down the pattern into 5s –try and figure out

8 + 9 + 2*4
4*4 + 1 * 4 + 4
4*4 + 2*2 + 5

• I was really impressed with several students who shared strategies that were a bit slower, for instance counting every group of 5, without shame. I hope I can keep that culture going.

My students have already seen exponents for a few years (I teach 8th grade), and I’m curious how this would develop thinking differently for students who haven’t articulated the idea of an exponent. There’s definitely some element of intellectual need for it, but at the same time it doesn’t scream “this will make your life easier in the future”, which is something I want students to see when exploring a new concept.

Either way, kids really liked this, and there aren’t enough great visualizations of exponents out there. I’m excited to show them this one:

Number Sense – Number Talks 5/13

Number talk today:

Got a lot of great ideas. A few that struck either me or my students:

• Several students doubled, and then doubled again to make multiplying by 4 easier
• Using the distributive property to break apart 10 and the half seems like common sense, but it was a big hit in two classes. I’m beginning to think that a flexible understanding of the distributive property is a huge part of number sense
• Among students who prefer to operate with improper fractions, there is a divide between students who see the opportunity to simplify the fraction first (21/2 * 4/1 = 21/1 * 2/1)  rather than multiplying (one student converted to a common denominator of 4, for 84/4, then multiplied 84 * 4 and divided by 4*1). These are the valuable shortcuts that a) make calculation easier, but b), and more importantly, show an understanding of algebraic structure, in particular the critical importance of the commutative and associative properties when working with fractions.

On this note, I’ve been thinking more about the longitudinal structure of number talks. I’m structuring them day by day pretty randomly — whatever I think will be meaningful is what we think about. I’m curious if grouping them by structures I want students to see would be valuable. On the one hand, sustained practice with a mathematical idea could help solidify that idea, especially in lower-skilled students. On the flip side, math is math, and number talks as mixed practice have a lot of value in messaging math for math’s sake. On top of that, I’m not sure students could keep track of a weekly theme for number talks, the unit we’re in for the rest of class, and then a range of topics for warm-ups and the rest of their classes in a meaningful way. But maybe it’s something to think about.

Number Sense – Division, Axes, Nerd Search

Wow. Quite a day. State testing (here, MCAS) is tomorrow. I believe teachers set the tone for kids, and I’m doing my best to make them feel calm and centered heading into tomorrow.

Division
Number talk today:

A few surprises:
How many student found the precise answer
How many of those students (almost all) expressed their answer as a decimal
How many of the students who chose to use an estimation strategy are my top students
How many students chose to think about it in terms of multiplying 9 by an unknown to get 1001, rather than division.

The last one is the most interesting to me. Division is defined (in rigorous mathematics, anyway) as no more than the inverse of multiplication). I think I’m happy that that is deep in the number sense of a number of my students. That said, division has got to be one of the basic procedures students do day in and day out that has the most possible representations and interpretations.  Need to find some more number talks to get at that ambiguity. Makes me think of this number talk, from Fawn, and how it could be adapted for a visualization of division.

Axes
This question was the focus of class today

These 8th graders are having a really tough time with linear equations on axes with a scale other than 1 to 1. They love counting boxes to find slope, and get confused when that doesn’t work. And this is our fault — spending too much time on that procedure, and too many questions out of context (like the one above!) And it’s great that they can reliably find slope on a conventional coordinate plane, but when we think about concepts that students will apply in the real world, finding the slope on an Algebra textbook-style coordinate plane will probably never happen. The application of the principle of rate of change absolutely will. Which one are we preparing kids for? And what does preparing kids for the second one look like? That’s my tough question of the day. It’s a critical form of number sense, and I’m worried my students don’t have it and I don’t know how to teach it beyond saying here, think about this.

Nerd Search
Wrapped up class today by sharing Bill Amend’s Nerd Search from his Foxtrot comic.

Inspired by his talk at NCTM, I’ve been showing some of his nerdier comics to my students. I planned a bit of a shorter lesson today, and just planned to give the nerd search to a few students when they finished their problem set, but it ended up engaging a ton of students and inspiring a spirited discussion to end class. One student came up to me after class and asked how many she had to do (she’s a very conscientious student, but not usually especially motivated to work when she doesn’t need to). I told her it wasn’t homework, but she should try as many as she could if it made her happy. She said she wanted to get all of them, and made me explain the integral and sum. Then, feeling outworked by my students, I spent 20 minutes finding the square root of 375,559,383,241 by guess and check. I was successful! And grateful for the invention of calculators.

Number Sense – Number Talks 5/6

My best number talk today yet. Question here:

My current practice is to give students time to silently and mentally find an answer (in this case about 45 seconds), then we share out every answer before sharing strategies. In each class I got 6-10 different answers, and at least half of the hands shot up to share a strategy (I don’t know about your class, but that was pretty good for me).

A few of the strategies below for your enjoyment (I’m only including the correct ones, although the wrong ones were interesting as well, especially the fact that 10×10 – 7×7 came up several times).
4×10 + 5×5+ 10 + 5
4×10 + 10 + 6×4 + 11
5×10 + 5×4+ 5
10×10- 5×5
10×10- (1/4)*10×10
4×16 + 11
And plenty more, including one student who told me she counted every dot.

I was pleasantly surprised with the engagement in asking 8th graders to count dots on a page. Finding multiplicative structure in patterns of dots reflects the habits of mind students need to find structure in any mathematics — and to believe in their ability to find that structure.

Number talks using dots will come back, but one I’m not sure about is this, stolen from by Michael Pershan’s posts on exponents

 

I like it a lot, and I’m sure I’ll use it at some point. However, I value number talks because they promote flexible thinking with basic skills. I’m not sure how many different ways this can be interpreted — or, building off of that, another exponential pattern like this one (how many black triangles are there)

I’m curious what kids can do with these. Will post back when that happens.

 

Number Talks 4/29

Today, asked this question, from Fawn Nguyen

Got some really awesome answers. A bunch of estimates, including several who chose to estimate by finding 4 times 30, which coincidentally gives the exact answer of 120.

Had a tough time representing student ideas as they explained. For instance, in two classes a student presented an approach that I scribed like this:

3 x 32     = 96
1/2 x 32 = 16
1/4 x 32  = 8
= 120

Which was fine for representing the process, but what I want to get at ,and what is explicit in the Common Core definition of Look for and make use of structure (MP.7), is visualizing the distributive property, the idea that (3 + 1/2 + 1/4) = 3.75 — and maybe even representing the fraction-to-decimal conversion as well.

Beyond that, I’m curious what ways I can find to get other students to engage with that thinking. One student coming up with it and explaining it is one thing, and representing the mathematical structure helps as well, but it’s made me think more about having students write along with me to push them to engage with the ideas in the number talks. One big idea might just be to slow down and spend more time on fewer approaches.